

It's actually two- you think of it as a linear function that's been separated. This is going to have the distinctive V shape. Let's now look at f of x equals the absolute value of x. The domain is all real numbers, and so is the range. And we can see that it increases as we move from left to right. Notice that we have a section that's in quadrant I and a section that's in quadrant III. Another function that we want to be familiar with is f of x equals x cubed, also knows as the cubing function. We have a range from 0 to infinity, including 0, and we can see where it increases and decreases. The other thing to point out is that we have a domain of all real numbers. Its vertex will be at the origin, and we have this symmetry to the y-axis in this format. Now, this is going to have the shape of a parabola.
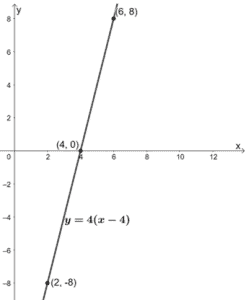
Let's start off with f of x equals x squared. That is, you should be familiar with them, but it's worth the time at the outset to make sure we're familiar with these different functions that we're going to use in this session. To begin with, let's review some functions that you should already have at your beck and call. We'll look at reflections, compressions and stretches, and then combinations of transformations. We'll look at vertical and horizontal shifts. Now, in particular, we're going to look at some specific types of transformations you can do on functions in order to change their graphs. During this session, we're going to look at a topic called transformations.


 0 kommentar(er)
0 kommentar(er)
